Su social network come Instagram e X alcuni di noi, a seconda degli interessi dimostrati nelle loro ricerche e interazioni coi contenuti, sono sommersi da immagini e video di gatti. Anche chi li detestasse, pur con una homepage a prova di felino, se decidesse di cercarli con gli appositi strumenti, si ritroverebbe comunque davanti a un'infinita carrellata di immagini dell'odiato animale. Ma come fa il social network a sapere che un’immagine ha a che vedere con la parola chiave “gatto”, magari perché rappresenta proprio un simpatico micio striato, o la scatoletta di cibo preferita del nostro animale domestico, mentre un’altra immagine rappresenta un cane, o della pasta al ragù?

Come fa l’algoritmo a restituirci delle immagini coerenti rispetto alla nostra ricerca?

Con i testi la faccenda è semplice: una ricerca sui documenti e a seconda di quante volte compare la parola cercata il testo sarà più o meno pertinente, ma un’immagine non ha al suo interno la parola “gatto”... O forse sì? I social media infatti barano, chiedendo ai loro utenti di descrivere l’argomento dei loro contenuti mediante l’utilizzo dei tag (nello specifico chiamati hashtag), parole chiave concise atte a didascalia che permettono di categorizzare i contenuti: quando cerchi gatto su instagram, stai fondamentalmente cercando immagini che abbiano il tag “gatto”, così come, se spesso guardi foto con questo tag, il social network prenderà nota delle tue preferenze e ti consiglierà contenuti che a loro volta siano stati taggati in questo modo. Ma un simile sistema dipende dall’onestà di chi carica i contenuti, e un altro individuo potrebbe malevolmente decidere di caricare una gran quantità di foto di gatti adornandole col tag “#cane”, per confondere alquanto le ricerche di un ipotetico zoologo alieno. La ricerca per immagini di Google infatti, e molte altre di questo tipo, utilizzano (fra le altre cose) un altro tipo di tecnologia, che fa uso di database vettoriali.

Ma cos’è un database vettoriale e perché, con l’esplosione dell’Intelligenza Artificiale (AI) se ne sente tanto parlare?

Un database vettoriale indicizza e memorizza gli embedding vettoriali per un recupero rapido e una ricerca per similarità. Un embedding vettoriale è una rappresentazione numerica di una serie di dati (ad esempio l’immagine di un gatto) trasformati in un vettore (cioè una lista ordinata di numeri) in uno spazio a più dimensioni. Questa rappresentazione è progettata per catturare caratteristiche, significati e relazioni del dato originale in modo che algoritmi di machine learning o sistemi di ricerca possano lavorare più facilmente su di essi. Qualunque sia il loro formato (testo, video, immagine) i dati, nell’ambiente informatico, alla fine sono una serie di bit, e come tali questo procedimento può essere attuato su ogni collezione di dati. Ad esempio, quando trasformi una parola o una frase in un vettore (come fa GPT), gli embedding vettoriali rappresentano il significato semantico del testo. Parole con significati simili come “re” e “regina” possono essere vicini in un embedding, mentre “gatto” sarà più vicino a “fusa”, “artigli”, “pelliccia” e “animale migliore del mondo”.

Un altro vantaggio della rappresentazione vettoriale è che offre una rappresentazione compatta e ricca di informazioni riducendo lo spazio occupato dal dato originale nella sua interezza (una sorta di riassunto ad alto rendimento). Una particolarità particolarmente apprezzata nel campo del machine learning dove i modelli hanno bisogno di una mole di dati enorme per potersi allenare efficacemente. La riduzione dei dati in embedding vettoriali riduce lo spazio economizzando sulle risorse utilizzate ed aumentando la velocità di esecuzione.

Ma come possiamo capire quando due vettori sono “vicini”?

Quando facciamo una ricerca, magari perché vogliamo trovare tutte le parole simili a “gatto” (come ad esempio “felino”), la nostra query viene a sua volta trasformata in un embedding, di modo che possa essere confrontata con gli altri embedding nel database per trovare i risultati più simili. Per comparare due vettori usiamo una funzione chiamata “similarità del coseno” (cosine similarity). La similarità coseno misura l'angolo tra due vettori nello spazio n-dimensionale e restituisce un valore tra -1 e 1 dove:

• 1 significa che i due vettori sono identici (stessa direzione).
• 0: significa che i due vettori sono ortogonali (completamente diversi).
• -1: significa che i vettori puntano in direzioni opposte.

Se visualizziamo i vettori come una serie di punti disposti su una linea, e per semplicità supponiamo ogni vettore composto di un solo punto, potremmo essere tentati di usare invece il teorema di Pitagora per calcolare la distanza tra due vettori. Questa soluzione ci darebbe la distanza euclidea, utile in alcuni ambiti ma non in quello che stiamo analizzando ora, dove la similarità del coseno è preferibile.

Facciamo un esempio pratico: immagina di avere queste parole rappresentate da vettori in uno spazio semantico a due dimensioni, dove ogni dimensione rappresenta una caratteristica del significato della parola. Supponiamo che il nostro modello assegni questi vettori:

• "cane" → (1,1)
• "gatto" → (2,0.5)
• "lupo" → (10,9)

Ora analizziamo cosa succede con le due misure:

Distanza euclidea:

La formula della distanza euclidea è:

$d(A,B)=\sqrt{(x2−x1)^2+(y2−y1)^2}$

Se calcoliamo la distanza:

• d(cane, gatto)$=\sqrt{(2-1)^2+(0.5-1)^2}=1.118033989$
• d(cane, lupo)$=\sqrt{(10-1)^2+(9-1)^2}=73$

La distanza euclidea dice che “cane” è più vicino a “gatto” rispetto a “lupo”.

Similarità coseno:

Ora calcoliamo la similarità coseno, che misura quanto due vettori puntano nella stessa direzione. La formula è:

$cos(θ)= \frac{A ⋅ B}{\parallel A \parallel ⋅ \parallel B \parallel}$

Calcoliamo per cane e gatto:

$cos(θ)= \frac{(1×2)+(1×0.5)}{\sqrt{(1^2 + 1^2)} \times \sqrt{(2^2 + 0.5^2)}} = \frac{2.5}{\sqrt{2} \times \sqrt{4.25}} ≈ 0.86$

Calcoliamo per cane e lupo:

$cos(θ)= \frac{(1×10)+(1×9)}{\sqrt{(1^2 + 1^2)} \times \sqrt{(10^2 + 9^2)}} = \frac{19}{\sqrt{2} \times \sqrt{181}} ≈ 0.99$

Dalla similarità coseno si evince stavolta che cane e lupo sono più simili rispetto a cane e gatto, ovvero hanno quasi la stessa direzione (1 se fosse proprio uguale).

Cosa rappresenta la "direzione" di un vettore?

Un vettore ha due proprietà fondamentali:

1. Lunghezza (modulo) → Quanto è grande il vettore.
2. Direzione → Dove sta puntando nello spazio.

Pensiamo ai vettori come frecce in una stanza:

• Se due vettori puntano nella stessa direzione, anche se uno è più lungo dell'altro, rappresentano concetti simili.
• Se due vettori puntano in direzioni opposte o ortogonali, significano cose diverse.

Nel nostro caso:

• "cane" e "lupo" hanno vettori con la stessa direzione, ma lunghezze diverse → Il modello capisce che sono concetti simili, anche se la distanza tra loro è grande.
• "cane" e "gatto" hanno vettori più vicini come valore assoluto, ma la direzione può essere diversa → Il modello li considera meno simili semanticamente.

Prendiamo invece come esempio un sistema che deve trovare la città più vicina a Roma. Abbiamo tre città con coordinate geografiche rappresentate da vettori:

• Roma → (41.9,12.5)
• Napoli → (40.8,14.3)
• Milano → (45.5,9.2)

Se usiamo la similarità coseno, potremmo trovare che Milano è più simile a Roma, perché le loro coordinate puntano in una direzione simile (verso nord Italia). Ma questo non significa che Milano sia vicina a Roma! Ecco dunque un esempio in cui, al contrario di prima, vogliamo proprio la distanza euclidea, perché ci interessa la prossimità fisica e non la direzione.

I modelli di cui parliamo in questo articolo sono più simili al primo esempio (con cani, gatti e lupi) piuttosto che al secondo, e per questo si avvalgono di database vettoriali con un sistema di ricerca che implementa la similarità coseno.

Ma fermi tutti: qualcuno potrebbe pensare che il primo esempio fosse sbagliato! Se infatti il cane, discendendo dal lupo, sia per qualcuno più simile ad esso rispetto al gatto, altri potrebbero obiettare che cane e gatto sono entrambi animali domestici, e in quanto tali più simili tra loro rispetto ad un selvaggio lupo!

Questo è solo apparentemente un errore e deriva dal fatto che l’ipotetico modello analizzato avesse solo due dimensioni (x,yx, yx,y), che nel nostro caso rappresentavano una caratteristica semantica come la specie come discriminante.

• Se il modello privilegia la specie:
  • "Cane" e "Lupo" risultano molto simili.
  • "Gatto" risulta meno simile a "Cane".
• Ma se il modello privilegiasse l’habitat o l'addomesticamento?
  • "Cane" e "Gatto" sarebbero più simili, perché sono entrambi animali domestici.
  • "Lupo" sarebbe più lontano da entrambi.

Abbiamo però detto che i sistemi possono avere molto più di una dimensione!

Cosa succede con più dimensioni?

I modelli di intelligenza artificiale usano spazi vettoriali ad alta dimensionalità (centinaia o migliaia di dimensioni).

In un modello con più dimensioni:

• Una dimensione potrebbe rappresentare la specie (cane e lupo vicini).
• Un’altra dimensione potrebbe rappresentare l’addomesticamento (cane e gatto vicini).
• Un’altra ancora potrebbe rappresentare la dieta, il comportamento, il suono che emettono, colore del manto, ecc.

La similarità coseno aiuta a trovare parole simili rispetto a un certo contesto, perché misura quanto i vettori puntano nella stessa direzione in quello spazio.

Per visualizzare l’utilità di più di due dimensioni possiamo prendere l’esempio dei colori, che codificheremo secondo le coordinate RGB, quindi tre dimensioni, un concetto che non sarà certo nuovo ad artisti, sviluppatori, fotografi e designer! La scomposizione in RGB significa la divisione del colore nella quantità dei tre colori primari (in digitale) che fungono da “componenti fondamentali” in un pigmento, dove 0 indica che quel colore primario non è assolutamente presente e 255 significa che è del tutto presente.

Il Nero sarebbe dunque (0,0,0), mentre (255,255,255) il Bianco, così come ad esempio il Magenta verrebbe codificato da (255,0,255) e lo Smeraldo da (80, 200, 120).

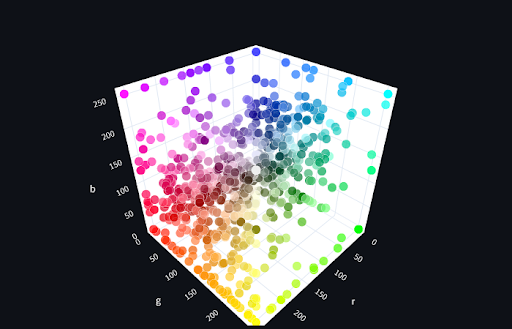
Dall’immagine è facile vedere come colori simili siano gli uni vicini agli altri ma su dimensioni diverse a seconda di diversi concetti di “similitudine”, e come tendano a formare dei “cluster” di dati simili tra loro (ad esempio i colori caldi tutti sulla sinistra in basso rispetto a i freddi a destra in alto).

Proviamo a fare una ricerca col metodo “standard” per il colore Rosso. La nostra ricerca, visualizzata nell’immagine qua sotto, mostra tutti i colori il cui nome contiene la parola “Rosso”: i risultati sono 51 e, dopotutto, in questo caso piuttosto coerenti.

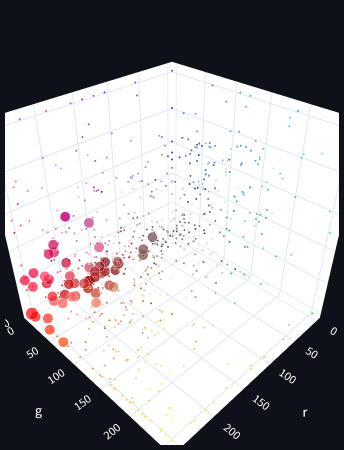
Tuttavia già da questo esempio si possono notare certe mancanze: alcuni dei colori più al centro dell’immagine, che la nostra ricerca ci ha restituito, sono forse più simili a un grigio caldo che non a un rosso, ed emergono tra i risultati solo perché contengono la parola “rosso” nel nome piuttosto che per vere e proprie qualità cromatiche, come la posizione nell’immagine stessa suggerisce.

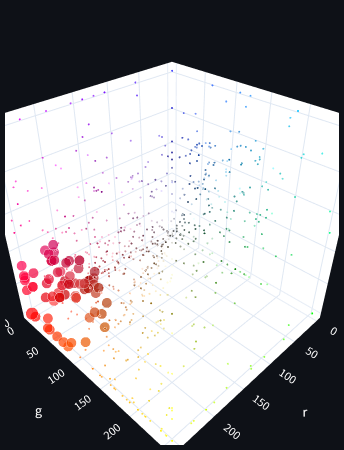
Al contrario ci sono parecchi arancioni, marroni e violetti che possiamo vedere nell’immagine dei colori completi qua sopra che sono indubbiamente molto vicini al rosso, ma che la nostra ricerca non ci restituisce poiché non hanno “rosso” nel nome. Con questo metodo, se uno studioso poco fantasioso avesse dato all’azzurro un nome come “colore che non è rosso”, paradossalmente l’azzurro comparirebbe tra i nostri risultati, avendo “rosso” nel nome, facendoci tutti dubitare di possibile daltonismo. Proviamo ora una ricerca per similarità coseno (l’immagine sotto): non solo in questo caso abbiamo più risultati coerenti (68), ma abbiamo anche eliminato quelli meno congruenti che la ricerca di prima ci mostrava comunque. Questo tipo di ricerca non ci restituirebbe un azzurro!

Questo ultimo esempio dei colori è stato preso dal sito huggingface.co dove le immagini sono in 3d e interagibili e inoltre si possono modificare i parametri di ricerca, dacci un’occhiata!

Abbiamo visto una rappresentazione intuitiva a tre dimensioni per i colori, potremmo aggiungerne una quarta rappresentante l’opacità! Quando però si passa ad altri tipi di dati, come il linguaggio naturale o le immagini complesse, il numero di valori necessari per una rappresentazione utile aumenta notevolmente. Le parole o interi documenti, per esempio, possono essere trasformati in vettori con centinaia di dimensioni (ad esempio 300 o 768), dove ogni numero cattura un aspetto specifico del significato del testo. Più numeri vengono utilizzati, maggiore è il livello di dettaglio che può essere catturato.

Il Trade-off tra Specificità ed Efficienza Computazionale

Aggiungere più numeri a un embedding consente di rappresentare con maggiore precisione le caratteristiche di un dato, migliorando la qualità della ricerca per similarità o la capacità di un modello di machine learning di distinguere tra concetti complessi. Tuttavia, questo ha un costo computazionale:

• Spazio di archiviazione: Un vettore a 300 dimensioni occupa più memoria rispetto a uno a 50 dimensioni.
• Velocità di calcolo: Il confronto tra due vettori richiede più tempo quando le dimensioni aumentano, poiché ogni operazione di similarità deve essere calcolata su più numeri.
• Effetto della "Maledizione della Dimensionalità": In spazi con molte dimensioni, le distanze tra i punti tendono a diventare meno significative, rendendo più difficile distinguere elementi realmente simili da quelli casualmente vicini.

Un vettore che descrivesse in tutto e per tutto il dato originale sarebbe grande esattamente come il dato stesso, e si perderebbe tutta l’utilità della riduzione in embedding vettoriale!

Per bilanciare questi aspetti, vengono utilizzate tecniche di riduzione della dimensionalità, come PCA (Principal Component Analysis) o t-SNE, che comprimono i dati preservandone le informazioni più rilevanti. Questi metodi aiutano a rendere gli embedding più efficienti senza perdere troppo in accuratezza.

In sintesi, scegliere il giusto numero di dimensioni per un embedding è una questione di compromesso tra una rappresentazione ricca di dettagli e la necessità di mantenere il sistema rapido ed efficiente.

Per concludere:

Non c’è dubbio che, database vettoriali o meno, le nostre homepage resteranno invase dai gatti, ed è giusto così: questi magnifici animali meritano la nostra più umile e servile adorazione.

Fatta però questa dovuta precisazione, era intento dell’autore non solo celebrare l’incontrovertibile superiorità felina, ma offrire un articolo che analizzasse in maniera semplice ma approfondita i concetti di database vettoriale ed embedding vettoriale.

Speriamo di esserci riusciti, ma se l’unica cosa che dovesse emergere da queste righe fosse la nostra adorazione per i gatti, ci riterremo soddisfatti comunque.